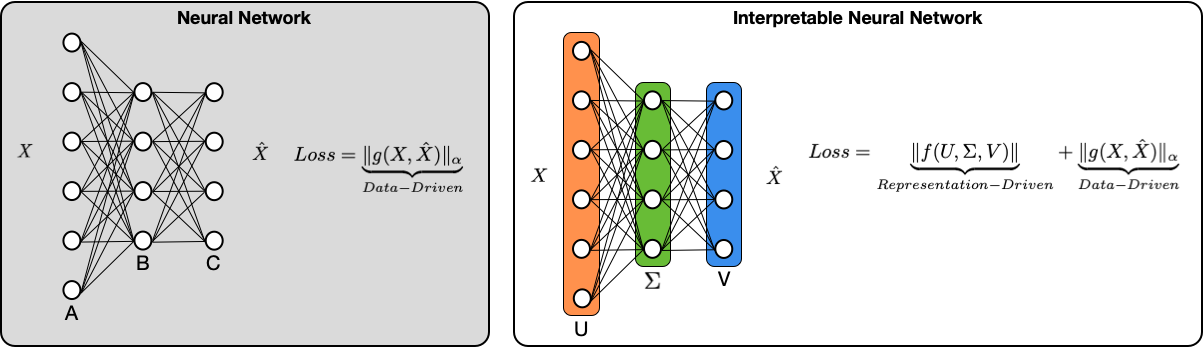
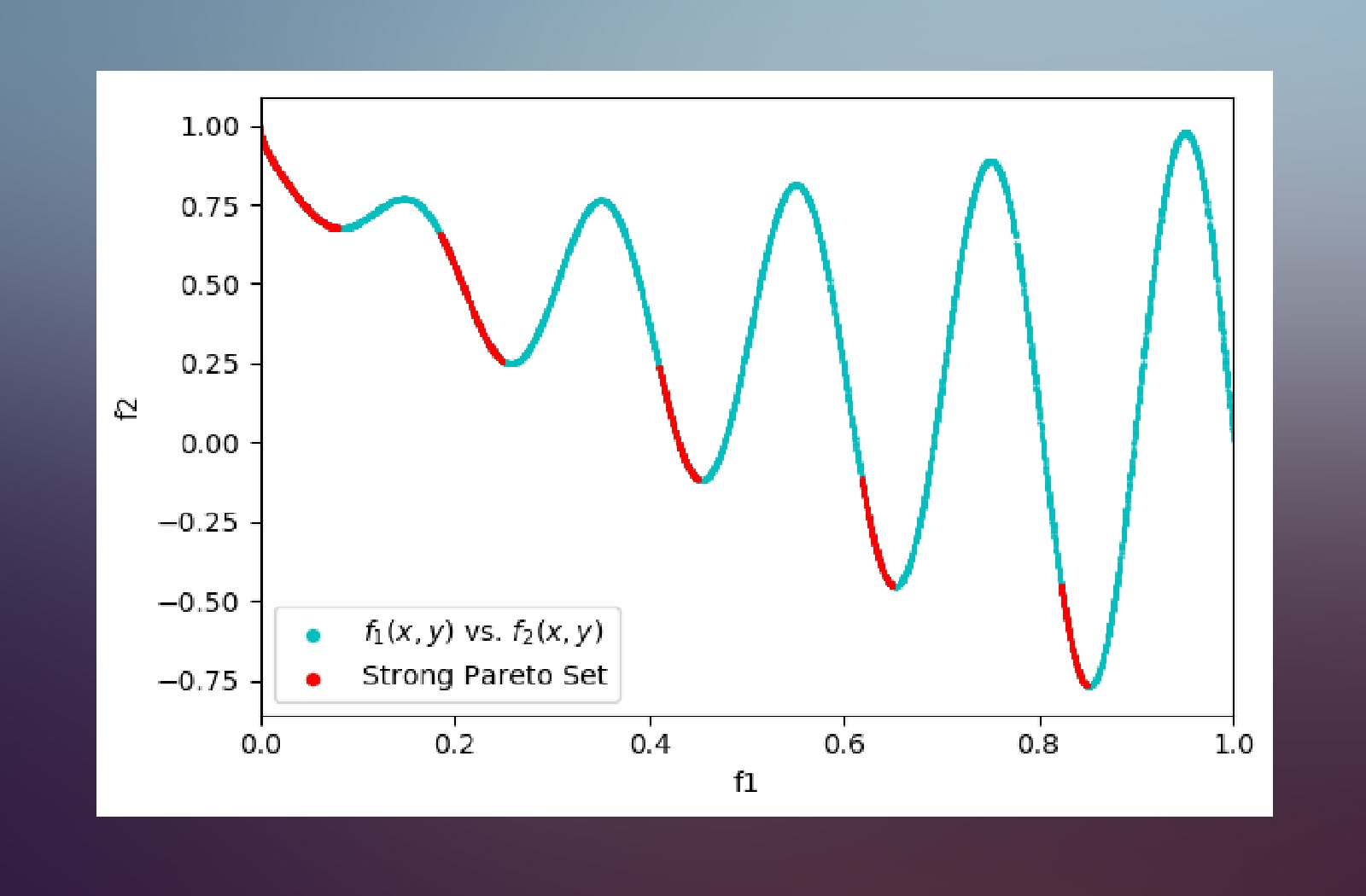
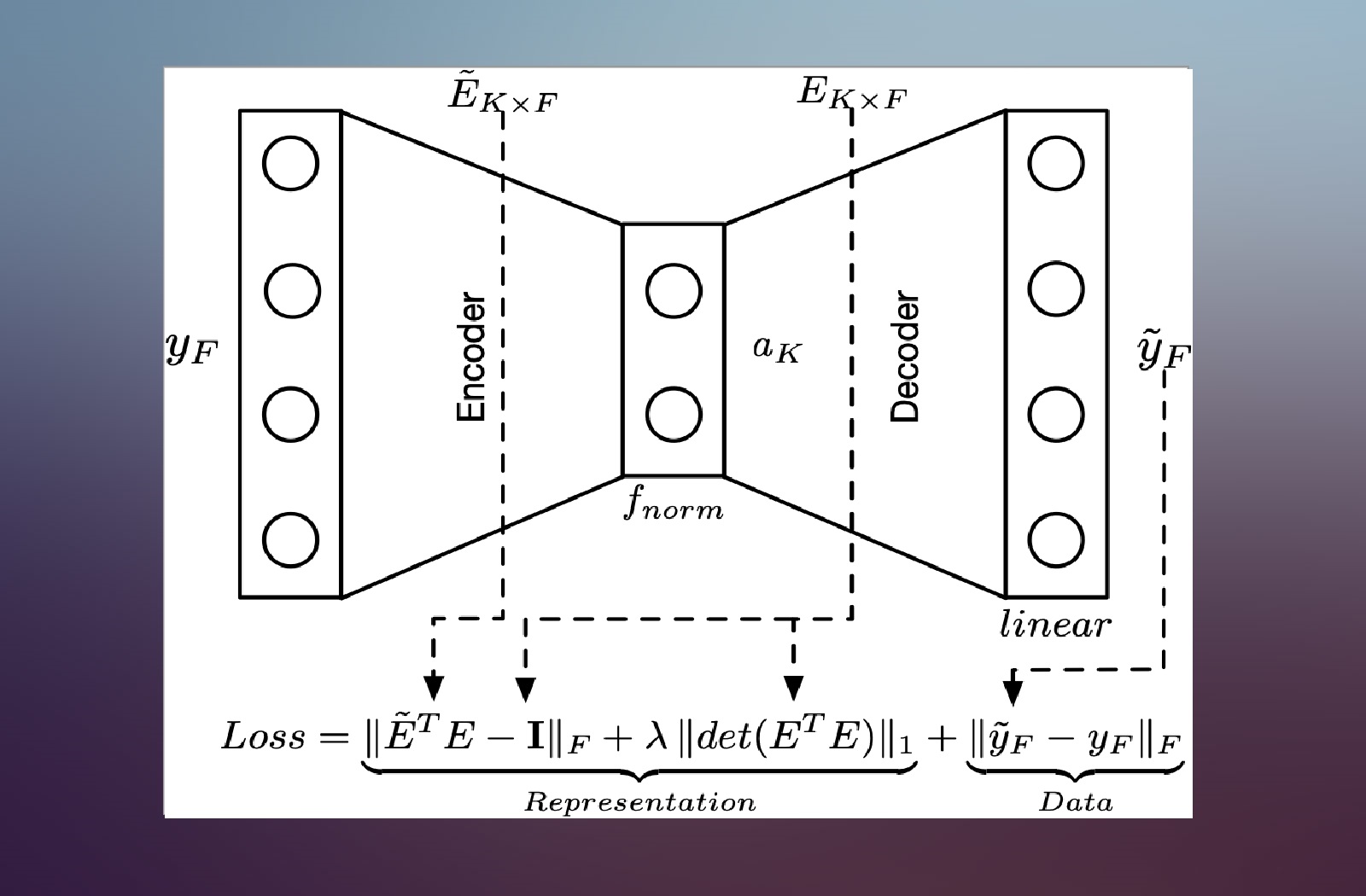
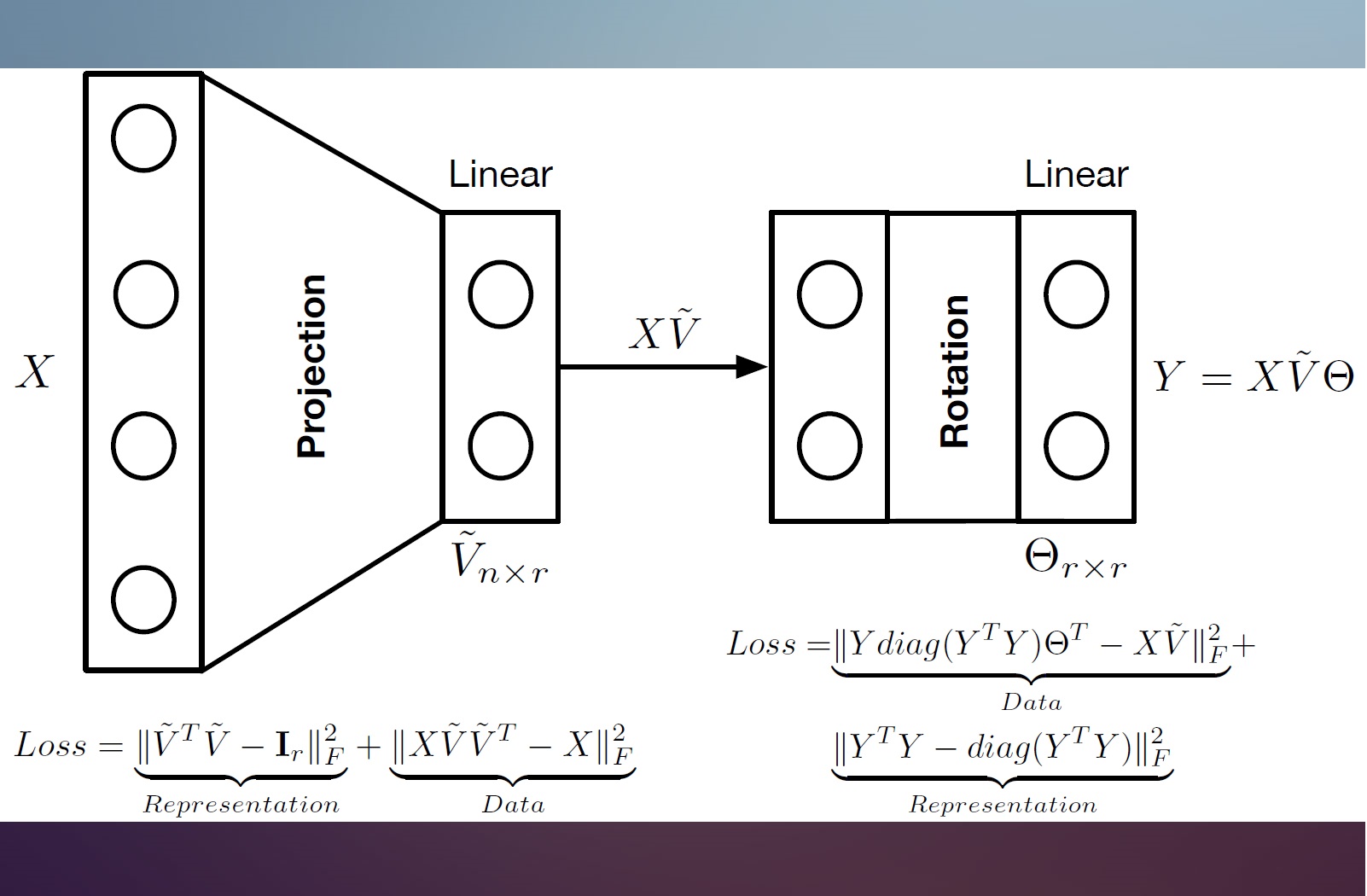
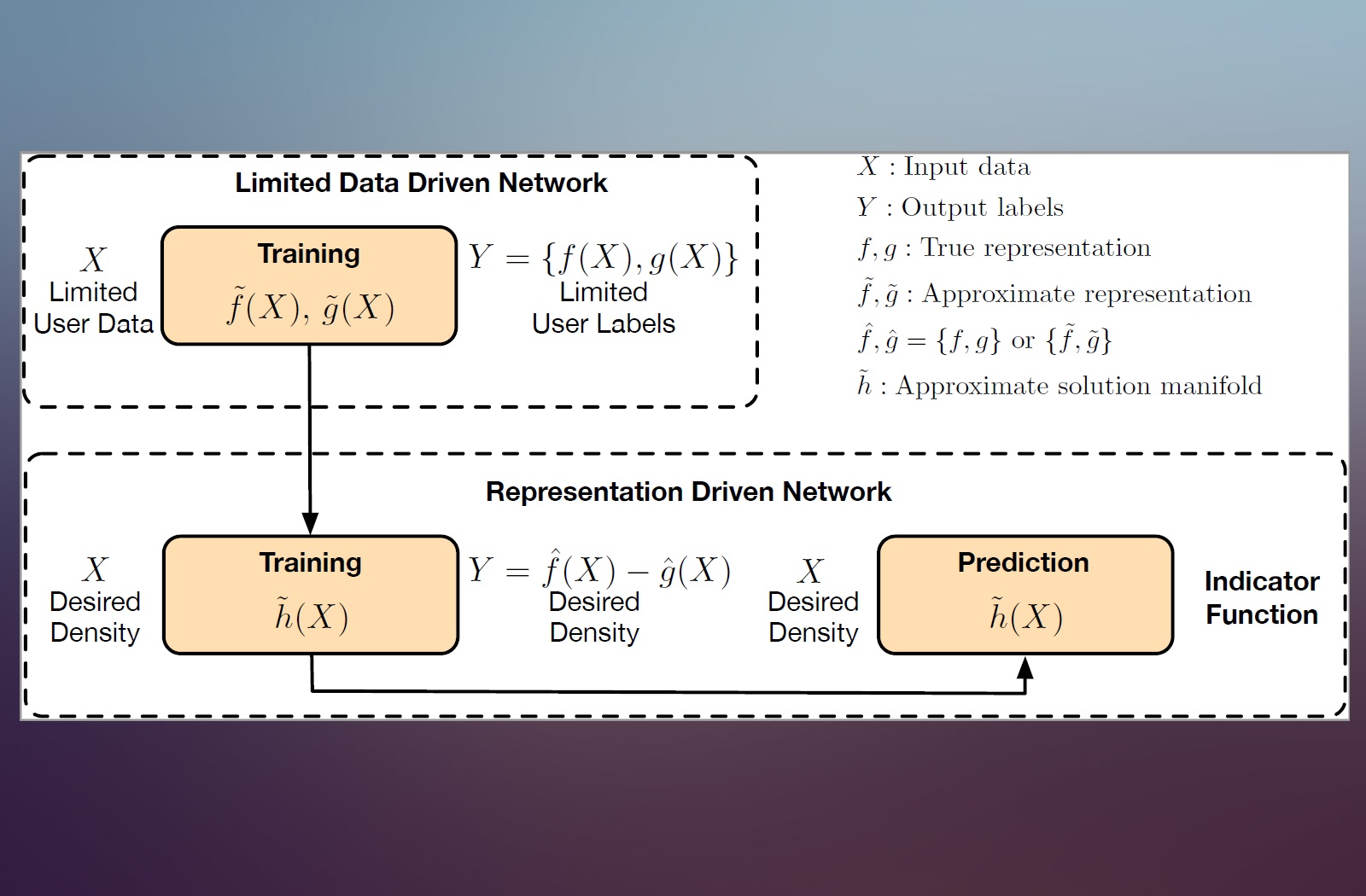
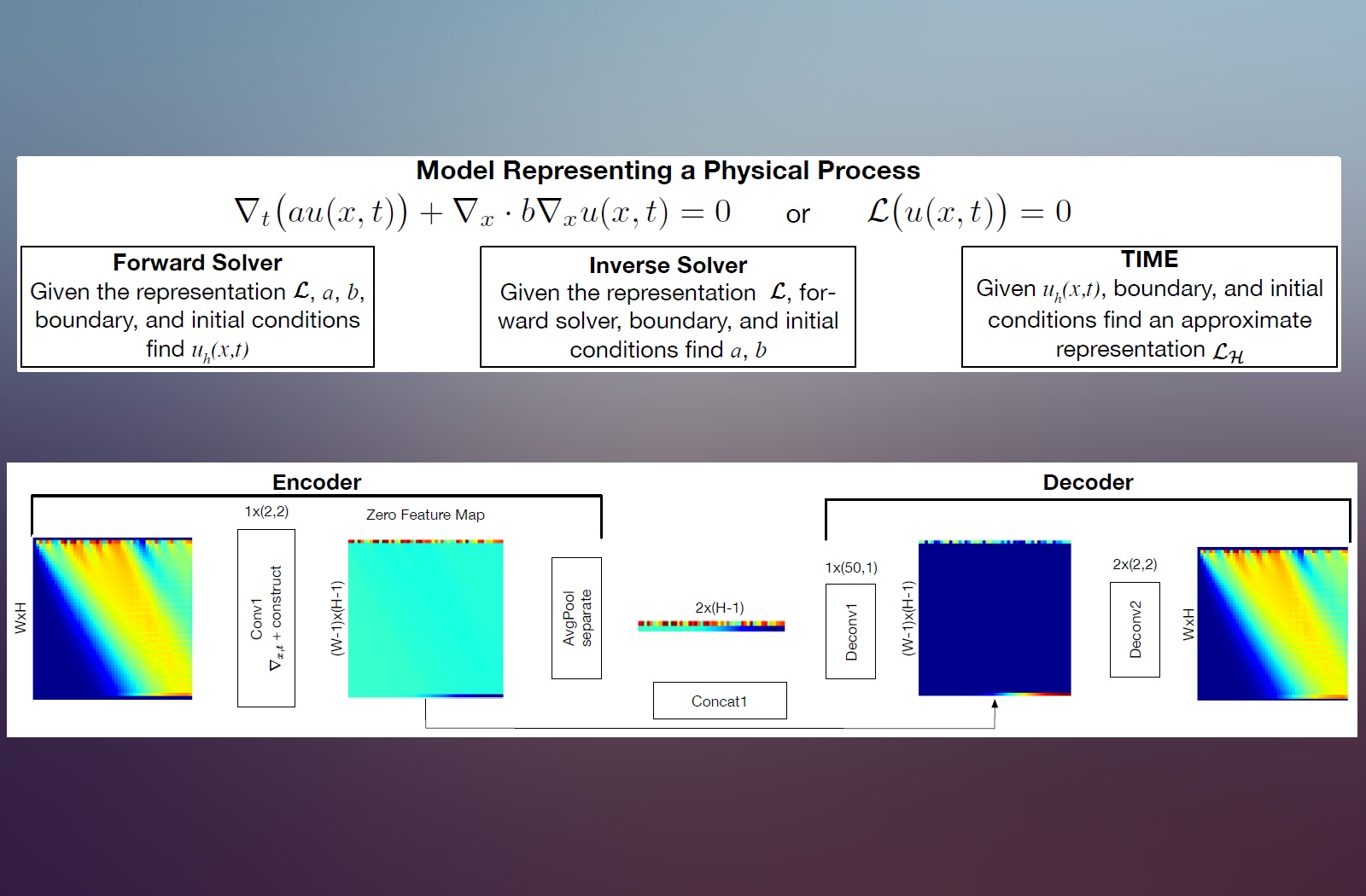
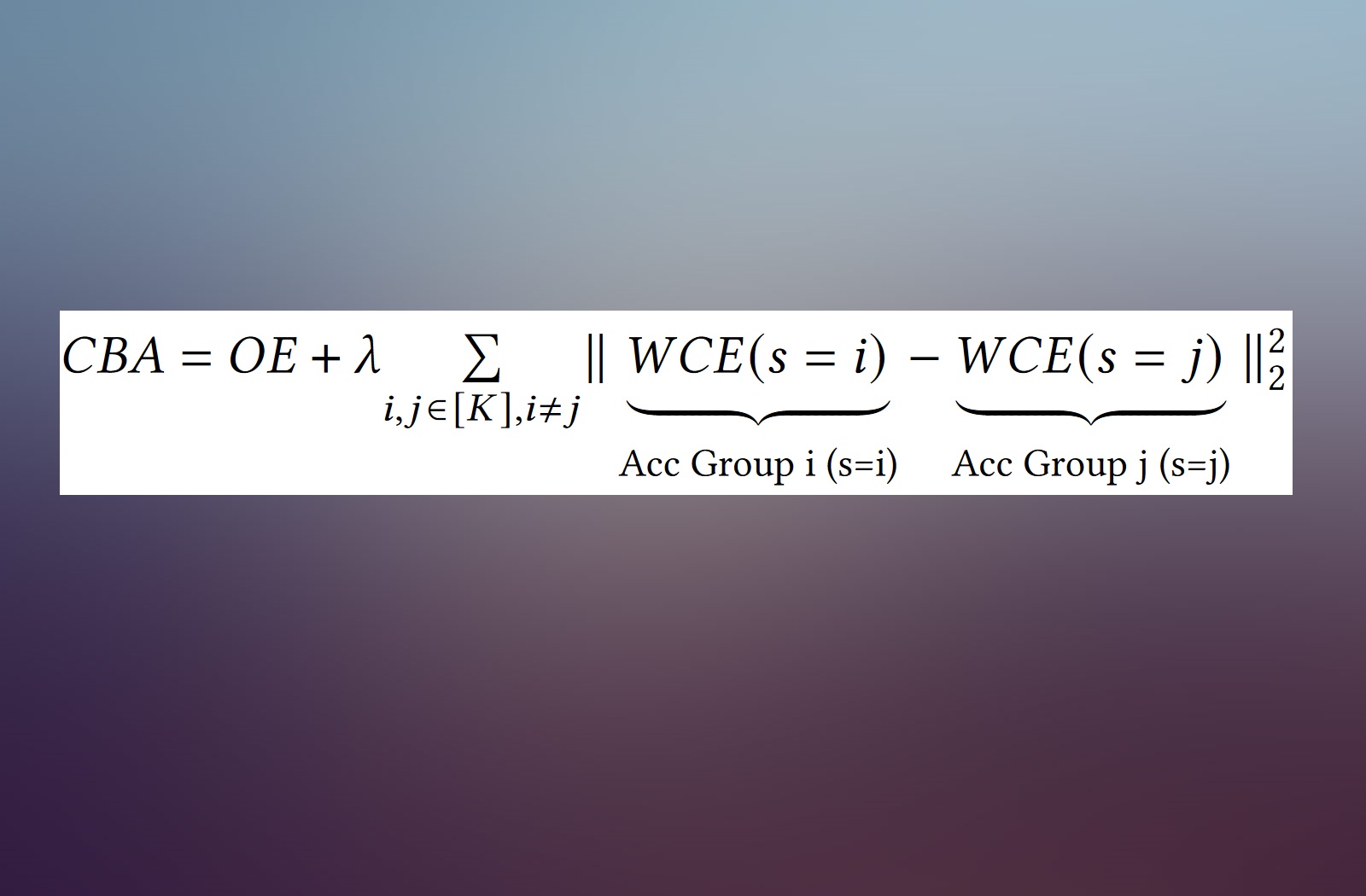Multi Task Learning and and Group-targeted Labels
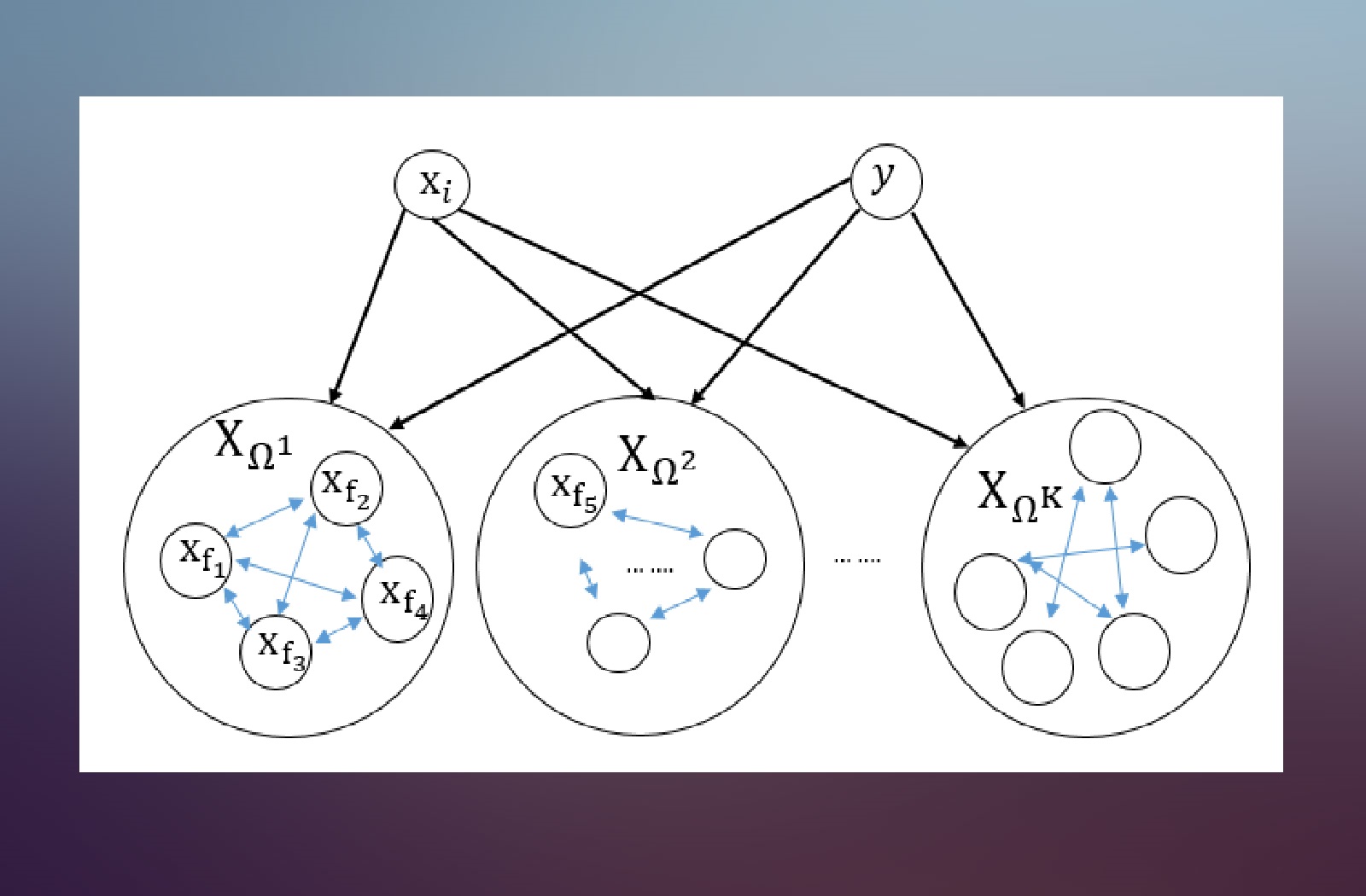
Multi Task Learning (MTL) paradigm is applicable a single data instance is associated with multiple labels or losses. MTL learns shared respresentations that are common across all tasks, while learning task-specific representations in individual branches. Our work explores untouched aspects of MTL, including i) cases where partial (sparse) labels are present, ii) designing scalable neural architectural frameworks and iii) training and evaluation of such networks under soft labels and iv) how MTL maps the input data to the output labels, specifically when the overall distribution is a mixture of several underlying distributions.